Research Highlights

Recent highlights of our science

Modeling the carbon cycle as a nonautonomous system

December 1, 2016

The terrestrial carbon cycle, like many biological systems, is commonly represented by compartmental models. Key metrics of the dynamics of such systems are transit time and mean age, which need not be the same. Under equilibrium, parameters describing the dynamics are constant in time, leading to models in the form of autonomous linear differential equations. With parameters and inputs that depend on time (e.g., under climate change), the compartmental models of interest are nonautonomous and are special cases of linear nonautonomous differential equations. We developed a theory for transit times and mean ages as nonautonomous compartmental systems. We employed the McKendrick-von Förster equation to show the mean age of mass in a compartmental system satisfies a linear nonautonomous ordinary differential equation that is exponentially stable. We applied this theory to study a nine-dimensional nonautonomous compartmental system modeling the terrestrial carbon cycle based on a modification of the Carnegie–Ames–Stanford Approach (CASA) model. We demonstrated that the nonautonomous versions of transit time and mean age differ significantly from the autonomous quantities when calculated for that model. For the nine-pool carbon model, results indicate that the average age of carbon stored on land is much larger than the average age of carbon leaving the land. We further showed that our nonautonomous theory generalizes the autonomous case.

Objective

To understand transit time and mean age dynamics of terrestrial carbon storage with time-dependent parameters and inputs.

Approach

  • We developed a theory for transit times and mean ages within nonautonomous compartmental systems.
  • We employed the McKendrick-von Förster equation to show the mean age of mass in a compartmental system satisfies a linear nonautonomous ordinary differential equation that is exponentially stable.

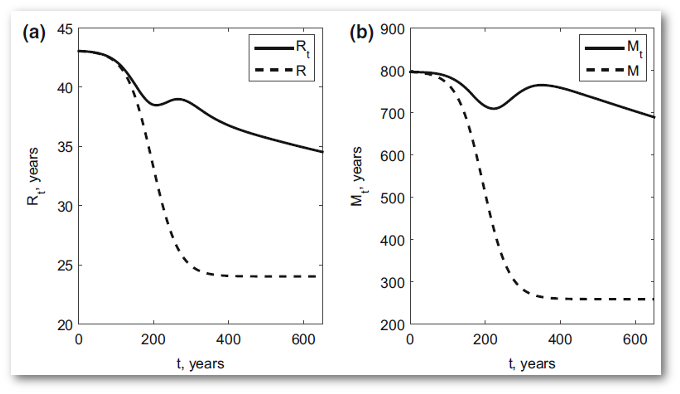Using our nonautonomous theory for representing a nine-pool terrestrial carbon cycle model, we showed an order of magnitude difference in the absolute values of mean transit time, Rt, and mean age, Mt. Moreover, significant differences were shown between these nonautonomous properties and the instantaneous quantities, R and M, which represent the autonomous model.

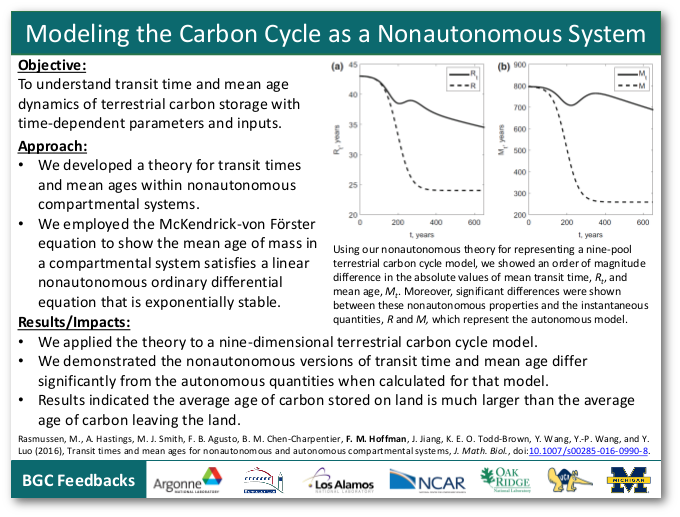
Using our nonautonomous theory for representing a nine-pool terrestrial carbon cycle model, we showed an order of magnitude difference in the absolute values of mean transit time, Rt, and mean age, Mt. Moreover, significant differences were shown between these nonautonomous properties and the instantaneous quantities, R and M, which represent the autonomous model.

Results/Impacts

  • We applied the theory to a nine-dimensional terrestrial carbon cycle model.
  • We demonstrated the nonautonomous versions of transit time and mean age differ significantly from the autonomous quantities when calculated for that model.
  • Results indicated the average age of carbon stored on land is much larger than the average age of carbon leaving the land.

Rasmussen, Martin, Alan Hastings, Matthew J. Smith, Folashade B. Agusto, Benito M. Chen-Charpentier, Forrest M. Hoffman, Jiang Jiang, Katherine E. O. Todd-Brown, Ying Wang, Ying-Ping Wang, and Yiqi Luo. December 1, 2016. “Transit Times and Mean Ages for Nonautonomous and Autonomous Compartmental Systems.” J. Math. Biol., 73(6):1379–1398. doi:10.1007/s00285-016-0990-8.